類比基礎知識 — 第 4 篇：最佳化三角積分 ADC 以實現低雜訊

編者說明：類比數位轉換器 (ADC) 可將類比世界連接至數位世界，因此對任何連接至真實世界的電子系統來說是基礎元件之一。此元件也是系統效能的重要決定因素。本系列文章將探討 ADC 的基礎知識、各種類型及其應用。本系列中第 1 篇的基礎知識探討了 SAR ADC。第 2 篇探討了三角積分轉換器。第 3 篇檢視了管線式 ADC。本文是第 4 篇，說明三角積分 ADC 如何能夠產生超低雜訊結果。第 5 篇將探討 SAR ADC 難以處理的輸入驅動問題。

三角積分 (ΔƩ) 積體電路拓撲持續出現於類比數位轉換器 (ADC) 中，為流程控制、精準溫度量測和稱重磅秤應用，提供高解析度、高整合度、低功率的解決方案。

這種轉換器玄妙的一點是，從 1 位元轉換開始，理論訊噪比 (SNR) 為 7.78 dB，相當於 5 V 系統中存在的 2 V (V_RMS) 雜訊。自此，該 ADC 能發展成真正的 24 位元三角積分轉換器，可提供 146 dB 的理論 SNR，相當於 5 V 系統中存在 244 nV rms 雜訊。

解析度從 1 位元躍升至 24 位元，乃是仰賴超取樣演算法、雜訊整型調變器與數位濾波器，來降低量化雜訊並提高 SNR。只要改為使用放大器輸入級饋入到 12 或 16 位元連續漸近暫存器 (SAR) ADC，就有辦法避開 ΔƩ 轉換器的複雜性及相關的雜訊。此設計路徑能發揮作用，但需要在電路板上使用更多積體電路，還會增加物料清單項目。

更佳的方法是直接以超低雜訊的 ΔƩ ADC 來解決雜訊問題。

本文將簡要探討低雜訊目標應用，以及如何在內部設計 ΔƩ ADC 來滿足這一要求。接著將介紹 Texas Instruments 的兩款 ΔƩ ADC (一款強調 24 位元精準性，另一款強調 32 位元精準性)，並說明如何利用這兩款產品穩健的數位濾波功能。

哪些情況適用 ΔƩ ADC

從類比的角度來看，工程師在測量溫度、壓力、荷重元與光學感測器的輸出時，需要各種不同的準確度。基本上，放大器讓設計人員更能量化這些微小且在多數情況下接近 DC 的類比事件。與時俱進的數位化技術改變了設計人員的觀點和能力，同時增強了儲存和修改感測器訊號的能力。

為實現數位擷取，典型的感測器訊號路徑從感測器開始，經過增益、多工和濾波器這幾個級，然後到達 ADC (圖 1a)。

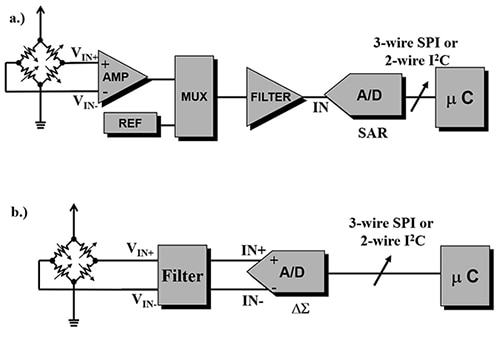圖 1：使用 SAR ADC (a) 或 ΔƩ ADC (b) 對感測器訊號進行數位化的兩種技術。對於高解析度電路，SAR ADC 需要放大並使用五階主動濾波器，而 ΔƩ ADC 需要前端類比一階被動濾波器。(圖片來源：A Baker’s Dozen: Real Analog Solutions for Digital Designers, B. Baker, ISBN 0-7506-7819-4)

圖 1a 中的轉換器是一個 SAR ADC，不僅能執行 12 位元至 18 位元轉換，而且能在高達 10 MSPS 的轉換速率下運行。16 位元轉換器可提供 2¹⁶ (65,536 個) 區段。在 5 V 系統中，最低有效位元 (LSB) 是 5 V/2¹⁶²⁹⁸，即 76.3 mV，理論 SNR 等於 98 dB。在 SAR 轉換器之前先運用類比增益，可實現更高的精細度。

ΔƩ 訊號鏈 (圖 1b) 透過單一轉換器改善了訊號鏈的解析度，這也減少了物料清單的項目。ΔƩ ADC 能提供 16 位元至 32 位元的轉換。在此訊號鏈中，24 位元 ΔƩ ADC 可提供 2²⁴ (即 16,777,216 個) 區段。在 5 V 系統中，LSB 因此為 5 V/2²⁴，即 298 nV，理論 SNR 等於 146 dB。此解析度級別使轉換器的精細度更接近感測器的能力。

24 位元的 ΔƩ ADC 比較慢，因為內部數位濾波器需要時間來執行濾波計算。此轉換器的典型輸出數據傳輸率範圍為幾 Hz 至 1 MSPS。請注意，類比濾波器現今是價格低廉的一階電阻電容 (RC) 濾波器，而不是具有三個運算放大器的複雜五階類比濾波器。

這兩種方法在雜訊上的差異很明顯，即 ΔƩ ADC 的低雜訊表現優於 SAR ADC (表 1)。

*注意：SNR = 6.02 N + 1.76，其中 N 是位元數

表 1：16 位元 SAR ADC 和 24 位元 ΔƩ ADC 的 ADC 區段、LSB 和理論 SNR，滿量程輸入電壓為 5 V。(資料來源：DigiKey)

在溫度、壓力與荷重元等感測器解決方案中，若速度規格不是非常關鍵，但準確度至關重要，ΔƩ ADC 則可提供出色的解決方案。這種 ADC 能透過數位 (而不是類比) 雜訊抑制技術，向下轉換為這些較小的電壓值。

ΔƩ ADC 的內部

ΔƩ ADC 內部有 80% 為數位技術。通常，轉換器會接收輸入訊號，並立即將該類比訊號轉變為數位訊號。然後，轉換器會將該數位訊號與後續的調變器轉換，合併至數位濾波器級中，累積的 1 位元訊號會在此級中變成多個位元。之後，轉換器會透過數位輸出級，將最終的多位元轉換連續傳送到正在等候的微控制器。

類比訊號首先會通過外部的一階抗交疊濾波器 (AAF)。然後，雜訊整型 (NS) 調變器會接收此類比訊號，並以轉換器的時脈速率，產生 1 位元流進入數位濾波器 (圖 2)。

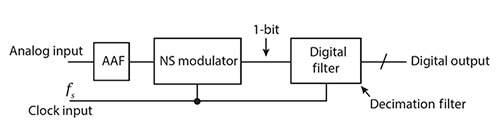圖 2：典型 ΔƩ 讓類比訊號通過一階 AAF，使用 NS 調變器產生 1 位元流，然後在連至微控制器的數位輸出端產生一個多位元結果。(圖片來源：CMOS: Mixed-Signal Circuit Design, 2^nd Edition, J. Baker, ISBN 978-0-470-29026-2)

數位濾波器從 1 位元流在多個程式碼中設定時脈，並在數位濾波器中產生完整的多位元結果。這些多位元結果會透過數位輸出連續地傳送。

ΔƩ 調變器

積分器／回授迴路的數量決定了 ΔƩ 調變器的階數。一階 ΔƩ ADC 調變器有一個積分器和回授迴路 (圖 3)。

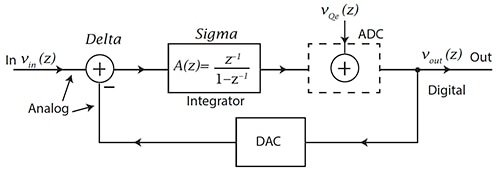圖 3：帶有類比積分器的一階調變器，以及 1 位元 ADC 和位於回授迴路中的 DAC。V_Qe(z) 是量化 ADC 雜訊。(圖片來源：CMOS: Mixed-Signal Circuit Design, 2^nd Edition, J. Baker, ISBN 978-0-470-29026-2)

在圖 3 中，類比訊號 (V_IN(z)) 會進入調變器的三角 (Δ) 部分。然後，類比訊號會通過積分器級 (即 Ʃ 級)，前往 1 位元 ADC (取樣率為 f_S，如圖 2 所示)，該 ADC 可以是比較器。這個現已建立時脈的數位化訊號，會回授到 1 位元的數位類比轉換器 DAC，也會繼續前往 Δ 級中的 V_OUT(z)。1 位元 DAC 提供了一個將從類比輸入訊號 V_IN(z) 中減去的類比電壓。這個一階調變器的傳輸函數為：

 方程式 1

由於積分器和回授迴路的緣故，調變器會在本身的數位輸出數據流上實作雜訊整型演算法 (圖 4)。

圖 4：在 ΔƩ 調變器輸出端的雜訊整型函數中，雜訊傳輸函數 (NTF) 等於 1-z^-1，其中 0.5 正規化頻率等於 F_S/2。(圖片來源：Understanding Delta-Sigma Data Converters, Schreier, Temes, ISBN 0-471-46585-2)

在圖 4 中，雜訊整型特性是減少轉換 1 位元量化雜訊的第一步。隨著雜訊被成功推入更高的頻率，低通數位濾波器完成了雜訊抑制程序。

更高階的調變器中含有額外的積分器和回授迴路。例如，三階調變器有三個積分器和三個回授迴路。透過減少 DC 附近的雜訊並增加整型雜訊，雜訊整型函數會隨著調變器的階數而變化。

更高階的調變器能提供更高的效能，但需要更多的矽硬體，且較不穩定、訊號範圍縮小。

ΔƩ 數位濾波器

ΔƩ ADC 是透過使用超取樣 (OS) 來運作。超取樣是調變器取樣率 (F_S) 與 ADC 輸出數據傳輸率 (F_D) 的比率，如方程式 2 所示：

 方程式 2

超取樣透過低通數位濾波器，對雜訊整型數據進行數位頻寬限制，來降低 ΔƩ ADC 的雜訊。

在 ΔƩ ADC 中，兩個常用的數位濾波器為 sin(pf)/pf (sinc) 和線性相位有限脈衝回應 (FIR) 濾波器。Texas Instruments 的 ADS1235 24 位元 ΔƩ ADC，以及 ADS1262 和 ADS1263 32 位元 ΔƩ ADC (ADS1263 整合了用於背景量測的輔助性 24 位元 ΔƩ ADC)，在數位濾波器實作上提供如下選擇：只使用 sinc 濾波器，或在 sinc 後方結合使用 FIR 濾波器 (圖 5)。

圖 5：ADS1235 24 位元 ΔƩ ADC 提供如下選擇：只使用 sinc 濾波器，或在 sinc 後方結合使用 FIR 濾波器。(圖片來源：Texas Instruments)

在圖 5 中，sinc (以「Sinc」表示) 濾波器是個低通數位濾波器。sinc 濾波器的輸出 (w(n)) 使用方程式 3 計算：

 方程式 3

z 域傳輸函數為：

 方程式 4

頻率響應為：

 方程式 5

在圖 5 中，Sinc^N 等於串聯 N 個相同的 sinc 濾波器。sinc 濾波器的振幅-頻率響應對照圖中，有著梳齒般的型式 (圖 6)。

圖 6：在 2400 SPS 的 ADS1262/63 中，許多 sinc 數位濾波器會產生梳齒般的頻率響應，在這些濾波器中，sinc2 等於串聯兩個相同的 sinc 濾波器，sinc3 等於串聯三個相同的 sinc 濾波器，以此類推。(圖片來源：Texas Instruments)

在圖 6 中，峰值和零點是 sinc 濾波器響應的特性。頻率響應零點發生於 f (Hz) = N ·F_D，其中 N = 1、2、3...。在零點頻率下，濾波器為零增益。

串聯的 sinc 濾波器會產生更高的衰減，從而增加延遲時間。舉例來說，如果在某個外部時脈速率為 7.3728 MHz 的特定 sinc 濾波器計算中，產生的輸出數據傳輸率為 14400 SPS，則第二個 sinc 濾波器的輸出數據傳輸率為 7200 SPS。

低通 FIR 濾波器是一個以係數為基礎的濾波器。該濾波器具有 50 Hz 和 60 Hz 的同步衰減頻率，以及數據傳輸率為 2.5 SPS 至 20 SPS 時的諧波。FIR 濾波器數據傳輸率的轉換延遲時間，等同於單次循環。FIR 濾波器從 sinc 濾波器接收預先經過濾波的數據，並將數據降頻取樣，以產生 10 SPS 的輸出數據傳輸率 (圖 7)。

圖 7：在 ADS1262/63 中，FIR 濾波器衰減了 50 Hz 和 60 Hz 訊號以減少線頻干擾，並提供一系列的響應零點，置於這些頻率附近。這些零點在 50 Hz 和 60 Hz 諧波處重複。(圖片來源：Texas Instruments)

FIR 濾波器衰減了 50 Hz 和 60 Hz 訊號以減少線頻干擾，並提供一系列的響應零點，置於這些頻率附近。響應零點在 50 Hz 和 60 Hz 諧波處重複。

精準低雜訊 ΔƩ ADC

低雜訊 ΔƩ ADC 的一個很好的範例，是先前提過的 Texas Instruments 的 ADS1235 差動輸入 24 位元轉換器。

ADS1235 是一款精密 7200 SPS ΔƩ ADC，具有三個差動或五個單端輸入，以及一個整合式可編程增益放大器 (PGA)，其增益分別為 1、64 和 128。此元件還包含診斷功能，例如 PGA 超範圍和參考監視器。ADC 可為包括磅秤、應變計和電阻式壓力感測器的高精密度設備，提供高準確度、零漂移的數據轉換效能 (圖 8)。

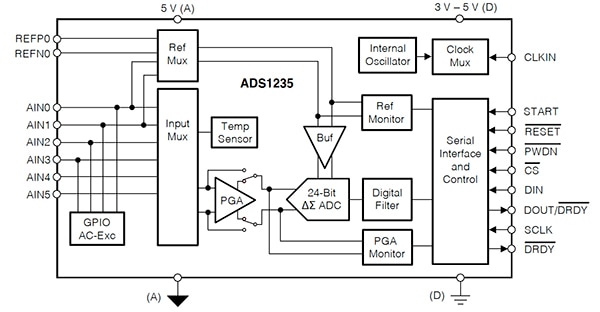圖 8：ADS1235 24 位元 ΔƩ ADC 方塊圖，其中有六通道類比輸入和 GPIO 輸入多工器。(圖片來源：Texas Instruments)

對於 ADS1235，影響雜訊效能的重大因素為數據傳輸率、PGA 增益和截波模式。較慢的數據傳輸率會引入數位濾波器的角頻率，因此能減少雜訊。此外，由於截波模式中執行兩點數據平均化，因此相較於一般作業，雜訊減少了 √2 倍。

憑藉低頻率、2.5 SPS 的數據傳輸率和 1 V/V 的 PGA 增益，5 V 系統中 sinc3 數位輸出的轉換器雜訊為 0.15 mV_RMS (0.3 mV 峰對峰 (_PP))，有效解析度為 24 位元，無雜訊解析度為 24 位元。此元件的理論 SNR 和實際 SNR 皆為 146 dB。事實上，在這些條件下，穩定的四階調變器與 sinc1 至 sinc4 濾波器，可產生 24 位元的有效解析度，以及 24 位元的無雜訊解析度。

對於 2.5 SPS 數據傳輸率，ADS1235 已實現近乎完美的 24 位元轉換。此系列的下一代 ΔƩ ADC 是 Texas Instruments 的 ADS1262/63。這些元件之間的主要區別在於 ADS1262/63 改善了低雜訊電路，並提供延伸的 32 位元輸出數據暫存器。

ADS1262/63 具有改進的低雜訊 CMOS PGA，增益分別為 1、2、4、8、16 和 32。彈性類比前端 (AFE) 含有兩個感測器激磁電流源，適用於直接 RTD 量測 (圖 9)。

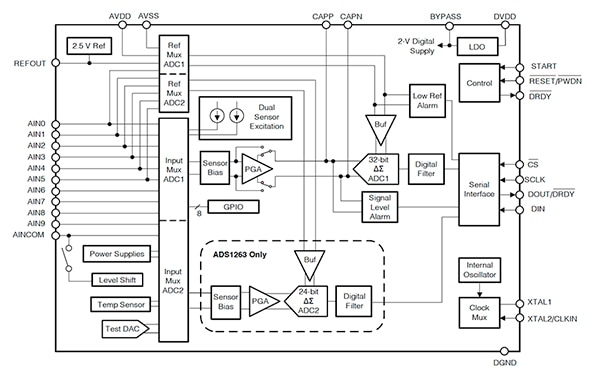圖 9：ADS1262 和 ADS1263 32 位元 ΔƩ ADC 方塊圖，其中有十通道類比輸入多工器。ADS1263 有第二個晶片上 24 位元 ΔƩ ADC。(圖片來源：Texas Instruments)

與 ADS1235 一樣，PGA 增益、數據傳輸率、數位濾波器模式和截波模式，都是影響 ADS1262/63 雜訊效能的重要因素。在 32 位元解析度下，ADS1262/63 著實展現了低雜訊深度能力。

首先，穩定的四階調變器與 sinc1 至 sinc4 濾波器，可產生 32 位元的有效解析度，以及 24 位元的無雜訊解析度。透過設定低頻率、2.5 SPS 的數據傳輸率和 1 V/V 的 PGA 增益 (旁通)，5 V 系統中 sinc3 數位輸出的轉換器雜訊為 0.08 mV_RMS (0.307 mV_PP)。此元件以 26.9 位元超越了有效解析度，並超越了 25 位元的無雜訊解析度。對於此 32 位元系統，理論 SNR 是 387 dB，實際 SNR 等於 164 dB。

24 位元與 32 位元轉換器在雜訊上的差異很明顯，即 32 位元 ΔƩ ADC 低雜訊能力優於 24 位元 ΔƩ ADC (表 2)。

*注意：SNR = 6.02 N + 1.76，其中 N 是位元數

表 2：ADC rms 雜訊、峰對峰雜訊和 SNR 的比較，滿量程輸入電壓為 5 V。(資料來源：DigiKey)

結論

隨著能力不斷增強，ΔƩ ADC 持續突破低雜訊極限。本文說明了這種近乎數位化的低雜訊 ADC，如何直接對應至溫度、壓力與荷重元應用中。文中對精密 24 位元 ΔƩ ADC 與 32 位元 ΔƩ ADC 進行基本的探討，概述實現超精準特性的途徑。