如何運用波德圖的威力，確保電路的穩定度

1930 年代，亨德里克·韋德·波德建立了一種直覺的增益／相位方法，目的純粹是為了讓電路穩定。此方法後來變成現今的波德圖，這種圖以直覺式圖形顯示電路或放大器的增益、相位，以及回授系統和過頻。

有鑑於波德圖的實用性和重要性，讓我們花點時間運用波德穩定性分析技術，來檢視開迴路放大器和電路回授因數強度，以分貝 (dB) 和相位響應 (度) 為單位。本篇部落格文章將檢視這些概念，並給出相關建議，幫助在以頻率穩定度作為主要目標時，如何避免設計出「顫音」電路。

若要練習此技術，您可從 DigiKey Innovation Handbook 線上創新手冊的資源中，下載波德圖的可列印版本。

單極點波德圖

單極點電路配置可讓 DC V_IN 訊號直接前往 V_OUT，而輸入頻率較高時，V_OUT 等於零點 dB。波德圖的結構很簡單。Y 軸單位是對數頻率，而線性 X 軸是以 dB 為單位的增益，或者以度為單位的相位。設計波德圖時，可以套用很多方程式，但讓我們先切入到速解法。

波德圖簡單的原因在於，使用者只要一個直尺工具，並知道幾個規則，就能畫出圖來 (圖 1)。

圖 1：單極點波德圖顯示，強度和移相使用直線來說明電路的頻率和相位響應。(圖片來源：Bonnie Baker)

在圖 1 中，兩個圖代表單極點電阻/電容對的頻率增益關係和相位。上下圖的 X 軸頻率範圍介於 1 Hz 至 10 MHz。上圖 Y 軸的範圍介於 0 dB 至 100 dB，1 Hz 訊號值等同於 100 dB。此數值與增益係數 100,000 x V_IN 一致。藍色曲線是單極點在 f_P 或 100 Hz 時的增益響應，其中 R 等於 159 kΩ，C 等於 10 nF。

隨著頻率增加到超過極點頻率 (f_P)，藍色曲線以 -20 dB／十倍頻或 -6 dB／八倍頻的速率下降。此衰減率是第一個需記得的波德圖法則：電路中每個極點都以 -20 dB／十倍頻的速率下降，從極點頻率開始。因此，如果兩個極點在相同頻率範圍內衰減 V_OUT，則衰減率為 -40 dB／十倍頻。

圖 1 最下方的圖代表此單極點電路的相位。1 Hz 時，R/C 網路的相位是 0°。f_P (或此例中為 10 Hz) 之前的十倍頻時，單極點相位以 -45°／十倍頻的速率開始朝目標 -90° 下降。

有幾個規則適用於極點的相位響應。極點電路的第二個波德圖法則，是相位在 f_P 處等於 -45°。第三和第四個波德圖法則描述的是相位的衰減和完成點。單極點相位在極點頻率 (f_P) 之前的一個十倍頻開始下降，最後在 f_P 之後的一個十倍頻，安定於 -90°。

單零點波德圖

單零點波德圖反映出單極點波德圖的相反法則。位置發生轉換，R 和 C 的數值相同，以預防 DC V_IN 電壓，同時讓更高的頻率通過電容 (圖 2)。

圖 2：單零點波德圖顯示了強度和移相。(圖片來源：Bonnie Baker)

隨著頻率增加到超過 f_Z，藍色曲線會以 +20 dB／十倍頻的速率上升。圖 2 最下方的圖代表此單零點電路的相位。在 f_Z 之前的十倍頻，單零點相位以 +45°／十倍頻的速率開始朝目標 +90° 上升。零點電路相位在 f_Z 處等於 +45°。

圖 1 中的數值概述如下：極點位置是 f_P，而 f_P 之後的增益強度，其斜率為 -20 dB／十倍頻。相位通過 f_P 的斜率為 -45°／十倍頻，相位以 0.1x f_P 開始衰減，並在 10 x f_P 時安定於 -90°。圖 2 中的數值概述如下：零點位置是 f_Z，而 f_Z 之後的增益強度，其斜率為 +20 dB／十倍頻。相位通過 f_Z 的斜率為 +45°／十倍頻，相位以 0.1 x f_Z 開始衰減，並在 10 x f_Z 時安定於 +90°。

放大器開迴路波德圖

從 sub-Hz 到零點 dB 截止頻率，標準運算放大器產品的頻率作業可在傳輸函數中具備多個極點和零點。放大器波德圖不存在神奇的魔法；照規則做即可 (圖 3)。

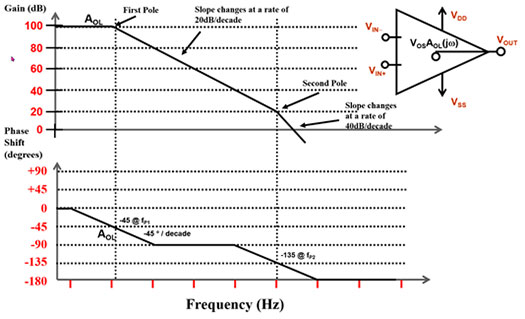圖 3：運算放大器的可能波德圖顯示了強度和移相。(圖片來源：Bonnie Baker)

圖 3 顯示一個運算放大器範例，其中傳輸函數有兩個極點 (f₁ 和 f₂)。藉著這兩個極點，增益每次下降 -20 dB／十倍頻，而相位總共下降 -180°。

此時，對於如何建構波德圖，我們已有粗淺的瞭解，現在讓我們看看實際的情形，其中混合了回授系統。

封閉迴路放大器的系統穩定度

如果花點時間查看運算放大器的電路，總會發現回授網路。傳統的運算放大器回授網路具有正向增益元件 (A_OL(jω)) 和回授元件 (β(jω))。

圖 4：典型的運算放大器回授網路具有前授式元件 (AOL(jω)) 和回授元件 (β(jω))。(圖片來源：Bonnie Baker)

在圖 4 中，運算放大器 (A_OL) 的開迴路增益較大，而回授因數相對較小。此配置將輸出送回到反相端子，並產生負回授條件，其中此回授會使輸出受到控制。我們將使用 β 的倒數 (1/β)，來判斷運算放大器電路的穩定度。

最簡單的 1/β 計算方法是將源極 (稱為 V_STABILITY) 放在運算放大器的非反相輸入上。此計算策略將提供一個絕佳的途徑，有助判斷電路的穩定度 (圖 5)。

圖 5：非反相運算放大器電路 a.) 和反相運算放大器電路 b.)，其非反相輸入端都有 V_STABILITY 虛電壓源，以便能夠準確計算電路的 1/β 因數，即雜訊增益。(圖片來源：Bonnie Baker)

如果檢視圖 5 中的電路，則會注意到非反相端子到輸出端的回授電路是相同的。V_STABILITY 虛電壓源的位置能夠準確計算電路的 1/β 因數，即雜訊增益。

1/β 穩定度分析使用 V_STABILTIY。如果假設運算放大器開迴路增益為無限，兩個電路的傳輸函數等於：

方程式 1

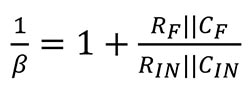方程式 2

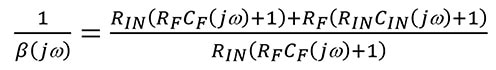方程式 3

當方程式 3 頻率分量 jω 等於零時：

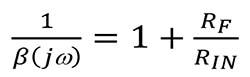方程式 4

隨著 jω 在方程式 3 裡接近無限：

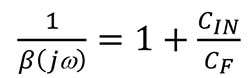方程式 5

1/β 的零點頻率 (f_Z) 和極點頻率 (f_P) 為：

方程式 6

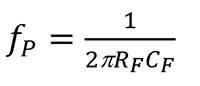方程式 7

對於遵循上方規則的 1/β 穩定度分析曲線，其波德圖顯示於圖 6 中。

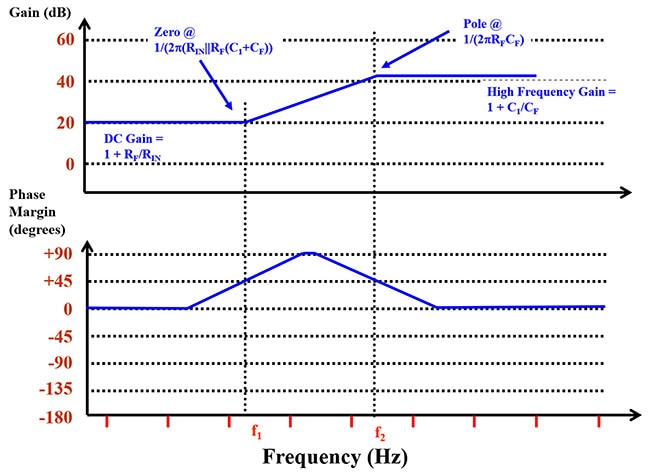圖 6：圖 5 a.) 和 b.) 的 1/β 頻率響應相同。零點發生在較低頻率，極點發生在較高頻率。(圖片來源：Bonnie Baker)

圖 6 描述運算放大器電路的 1/β (即雜訊增益) 之頻率及相位響應。此圖以圖形形式對方程式 4 至 7 進行概述。方程式 4 和 5 定義了 DC 增益和 ¥ 增益 (含)。方程式 6 和 7 確定了電路的零點和極點 (含)。圖 3 和 6 中的資訊可作為初始步驟，幫助建立運算放大器電路的穩定度，其中會定義系統的傳輸函數，以及極點和零點的位置。最後一步是將圖 3 和 6 疊加到一張圖中。

系統穩定度的測定

開迴路和封閉迴路增益的交點或接近率可定義電路的移相。一般來說，接近率小於或等於 30 dB 表示電路穩定。接近率大於 30 dB 時，電路狀況趨向於不穩定 (圖 7)。

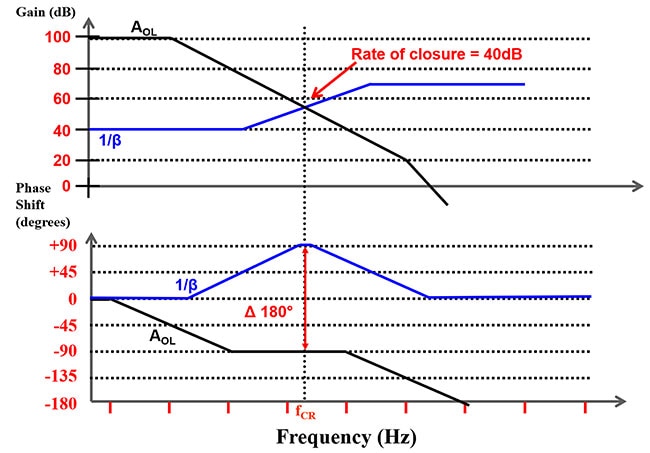圖 7：疊加之運算放大器的 AOL 增益和相位響應，帶有 1/β 增益和相位響應。(圖片來源：Bonnie Baker)

在圖 7 中，A_OL 和 1/β 增益曲線之間的接近率等於 40 dB。接近率 40 dB 表示移相大於 135°，這顯示出電路不穩定。藉由此配置，接近率 180° 會產生振盪電路。

以上問題有很多種解決辦法。透過移動極點頻率和零點頻率，可改變電阻值或電容值。另一個替代方式是選擇不同的運算放大器 (圖 8)。

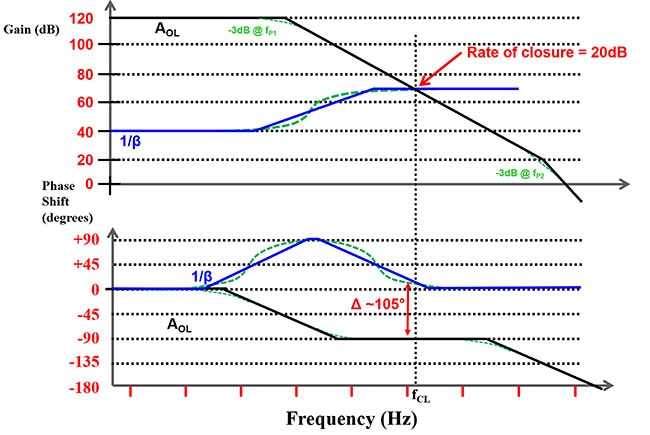圖 8：圖中使用的運算放大器，頻寬高於圖 7 中的運算放大器，且未改變零點頻率和極點頻率。(圖片來源：Bonnie Baker)

在圖 8 中，運算放大器的頻寬大約高出兩個十倍頻，而且未改變 1/β 網路。綠色虛線反映出實際的計算，並提供更實際的波德圖。放大器頻寬增加，可將接近率從 40 dB 變為 20 dB。產生的移相現在大約為 105°，表示電路很穩定。

圖 8 中的綠色虛線納入真實世界的響應，這些線超出尺和筆畫出的波德圖範圍。

測量電路增益和相位

要測量放大器電路的增益和相位，需要能提供輸入訊號的函數產生器，以及網路分析器 (圖 9)。此圖描繪的是 Tabor Electronics 的 LS3081B 3 GHz RF 類比掃描函數產生器。

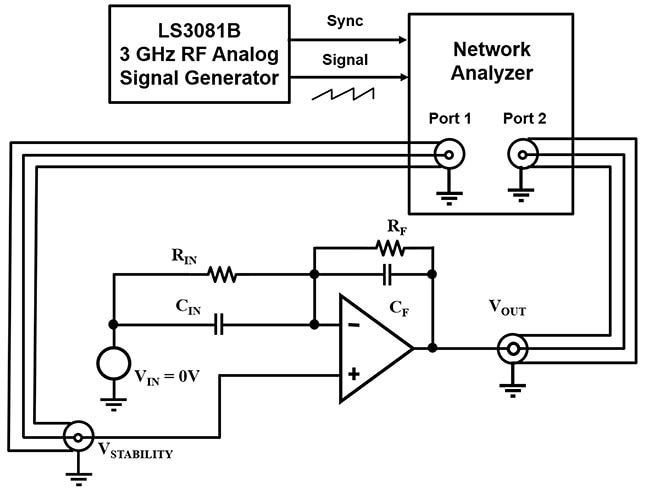圖 9：圖 5 b.) 之反相放大器電路的增益與相位測量配置。(圖片來源：Bonnie Baker)

在圖 9 中，函數產生器的輸入訊號是在埠 1 施加至 V_STABILITY 節點。訊號透過放大器電路傳播到電路的輸出 (V_OUT)，其中網路分析器會在埠 2 擷取訊號，並將其與函數產生器的埠 1 訊號進行比較。

結論

談到設計穩定的運算放大器電路時，波德圖是個非常有用的工具，值得添購。當您開始關注多極點和多零點電路時，波德圖背後的威力變得相當明顯。在此類電路中，放大器開迴路增益和回授網路間的接近率，能快速確定電路的穩定度。

這篇部落格文章展示了在方格紙上簡單利用直尺估算一階極點和零點電路的增益相位關係，這雖能有助於嫻熟使用波德圖，但最好的方法還是透過練習。您可以先從 DigiKey Innovation Handbook 線上創新手冊的資源中，下載波德圖的可列印版本。