Overview of Hexadecimal
2025-07-30 | By Nadir James
The Guide to Crushing the Hexadecimal Systems
If you've ever delved into mathematics or computing, you’ve likely encountered the Hexadecimal Number System. This base-16 system plays a crucial role in the world of technology, offering a convenient and efficient way to represent numbers. While it may sound complicated at first, don't worry—by the end of this guide, you'll have a solid understanding of how it works and why it's so important in computing. Whether you're a programmer, a student, or simply curious, this post will help you grasp the core concepts of hexadecimal and its practical uses.
What is a Hexadecimal?
The Hexadecimal Number System is a numeral system that uses a base of 16. Unlike our familiar decimal system (base 10), which uses digits from 0 to 9, hexadecimal utilizes 16 distinct symbols: 0, 1, 2, 3, 4, 5, 6, 7, 8, 9, A, B, C, D, E, F, where the letters A to F represent the values 10 to 15, respectively. This system is frequently used in computing and digital systems because it’s more compact and easier for humans to read compared to binary. In hexadecimal, numbers can be easily converted to other number systems, such as binary (base-2), octal (base-8), and decimal (base-10). This makes hexadecimal a valuable tool for certain types of conversions in computing.
Why is Hexadecimal Important?
Unlike long binary numbers, hexadecimal numbers are shorter and more manageable, making them easier for humans to read and work with. A single hexadecimal digit can represent 4 binary digits (bits), making it a more compact form for expressing large binary values.
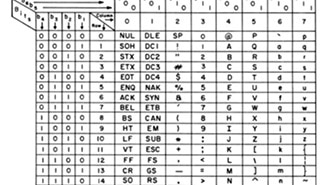
Table 1: Hexadecimal Number System Table
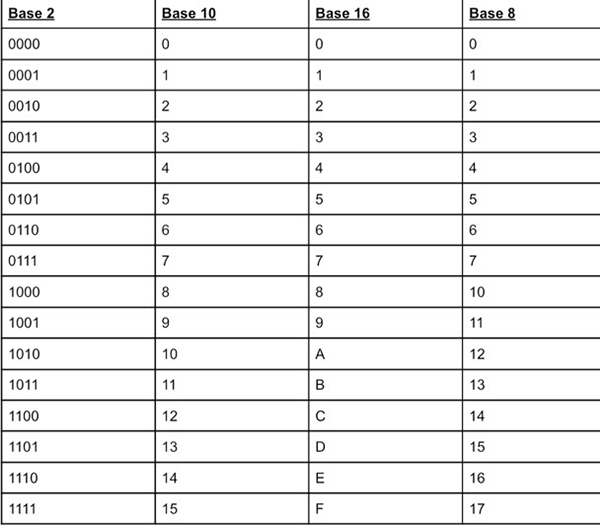
To help you visualize the differences between hexadecimal and other number systems, check out the following tables or DigiKey’s Number System Conversion Calculator, which shows conversions between hexadecimal, binary, octal, and decimal systems.
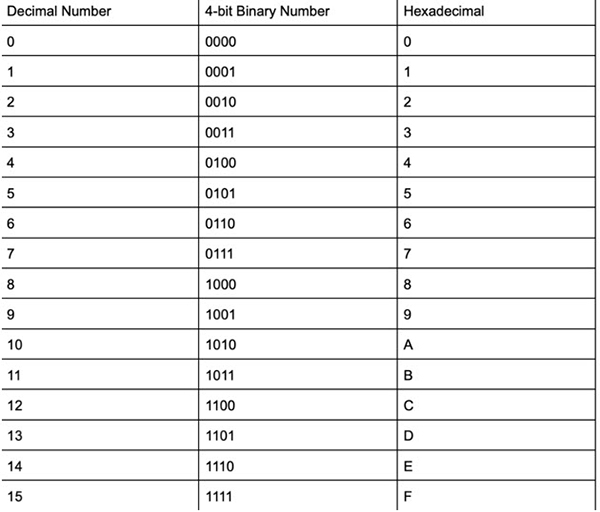
Table 2: Base Number System
Hexadecimal Number System Conversions:
Let’s dive into some examples of converting between different number systems using hexadecimal.
How to convert from Hexadecimal to Decimal?
Refer to Table 1
How to convert a Decimal to Hexadecimal? (Base 16)
Steps to convert below:
- First, divide the number by 16
- Take the quotient, then divide by 16 again
- Whatever remainder is left will produce the hex value needed for the answer
- Repeat the steps until you have 0 as the quotient
Example: Convert (1000)10 into hexadecimal.
Solution:
Step 1: Divided 1000 by 16
1000÷16 = ?
1000÷16 = 62 with remainder 8
Explanation: (62*16 = 992, 992+8 = 1000)
Step 2: Divide again
62÷16 = ?
62÷16 = 3 with remainder 14
Explanation: (3*16 = 48, 48+14 = 62)
Step 3: Convert to Hexadecimal
14=E (Refer to Table 2)
Step 4: Divide again
3÷16 = ?
3÷16 = 0 with remainder 3
Explanation: (3÷16 = 0, we stop here because the quotient is 0, 3 remains)
Step 5: Read the remainders from each step in reverse order
3>E>8 = 3E8
Final Answer: (1000)10 = (3E8)16
How to convert Hexadecimal to Octal?
Refer to Table 2
How to convert Octal to Hexadecimal?
Example: Convert (121)8 into hexadecimal.
Solution:
Step 1: Convert 121 to decimal (base 10).
8110 = 1(82) + 2(81) + 1(80)
8110 = 1(64) + 2(8) + 1(1)
8110 = (121)8
Step 2: Now convert 8110 into a hexadecimal (base 16).
Step 3: Divide 81 by 16 +
81÷16 = ?
81÷16 = 5 with remainder 1
Explanation: (16*5 = 80, 80+1 = 81)
5÷16 = ?
5÷16 = 0 with remainder 5
Explanation: (5÷16 = 0, we stop here because the quotient is 0, 5 remains)
Step 4: Read the remainders from each step in reverse order
5>1 = 51
Final Answer: (121)8 = (51)16
How to convert Hexadecimal to Binary?
Refer to Table 1
How to convert Binary to Hexadecimal?
Example: Convert (110101101)2 to hexadecimal (base 16).
Solution:
Step 1: Break down the binary digits into groups of 4 bits (add leading zeroes)
=0000, 1010, 1101
Step 2: Convert each group into hexadecimal
Looking at Table 1, we see,
Binary 0001 = Hexadecimal 1
Binary 1010 = Hexadecimal A
Binary 1101 = Hexadecimal D
Get the answer by going in order from the first group to the last
= 1AD
So, (110101101)2 = (1AD)16
Review:
That pretty much sums it up! From programming to memory management, knowing how to work with hexadecimal simplifies many processes in the tech world. Keep exploring and practicing, and you’ll find yourself moving between binary, decimal, octal, and hexadecimal with confidence. The more you dive into these concepts, the clearer the inner workings of digital systems become. Keep learning and stay curious!