訊號處理簡介：移動平均濾波器

訊號與系統在電氣工程中屬於強大的概念。可讓我們針對資訊如何穿越電器元件及修改進行建模。更重要的是，只要我們瞭解電壓等訊號是如何受到不同電氣元件的影響後，就可設計電路隨意操控訊號。因此，我們如何透過多種電器元件的組合，如電阻、電容和運算放大器等，針對積分和微分等數學工具進行建模會非常有趣。

以下列電路為例說明 (圖 1)：

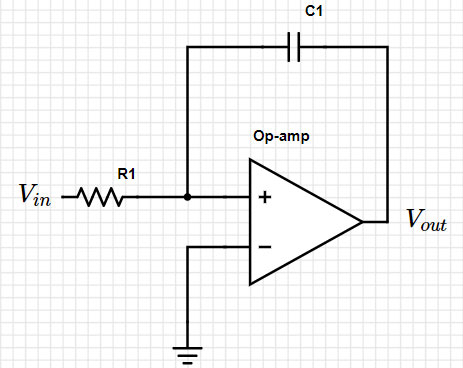圖 1：簡易的積分器電路。(圖片來源：Mustahsin Zarif)

在拉普拉斯域，我們可以用公式來代表電路：

Vout = -(1/s) (1/RC) Vin

在拉普拉斯域中，1/s 可實際對應積分！因此，我們就得到一個利用運算放大器的積分器電路模型。然而，當我們回到現實世界，系統總是會受到某種形式的隨機雜訊污染。

先不說積分器電路，以更簡單的例子來說明。試想有個電壓放大器電路，其輸入和輸出波形能以示波器測量，如圖 2 所示。

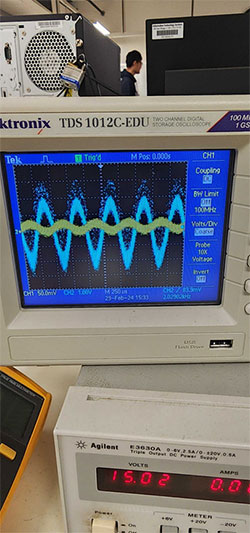圖 2：電壓放大器的輸入和輸出波形。(圖片來源：Mustahsin Zarif)

添加到底層可見正弦波形中的隨機雜訊，可能是由多種因素造成，例如因為電路建構在試驗電路板上，因此造成電氣連接不良。這種雜訊也會影響積分器的波形，我們將在此系列後續部落格文章中看到這一點。然而，我們通常較關注的會是如何將隨機干擾降至最低。

濾波技術

工程師喜歡採用濾波技術來克服這些障礙，這些技術可分為 1) 有限脈衝回應 (FIR) 濾波器，或 2) 無限脈衝回應 (IIR) 濾波器。

之所以稱為 FIR 濾波器，是因為輸出在任何時候都只取決於輸入的當前值和先前的值，而非仰賴輸出的過去值。因此具有無回授的非遞迴結構，能依此建立成如方程式 1 的模型。

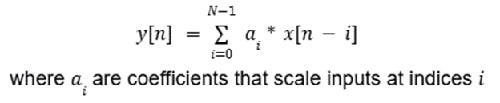方程式 1：FIR 濾波器的範例方程式。(圖片來源：Mustahsin Zarif)

積分器電路是 FIR 濾波器的範例之一，因為輸出僅取決於輸入。

另一方面，IIR 濾波器則具有回授，因為輸出在任何時候都取決於之前的輸出以及當前的輸入。可依此建立成如方程式 2 的模型。

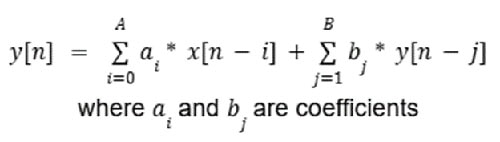方程式 2：IIR 濾波器的範例方程式。(圖片來源：Mustahsin Zarif)

圖 3 以方塊圖的視覺化方式呈現 IIR 濾波器，可顯示出輸入和輸出如何延遲 (z-i、z-j)、縮放 (ai、bj) 與加總，以得到呈現出的輸出。只要更改這些值，就可實作不同類型的濾波器。

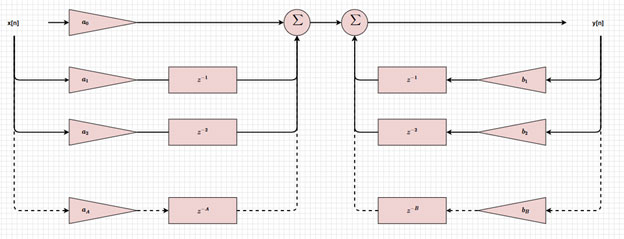圖 3：IIR 濾波器的方塊圖。(圖片來源：Mustahsin Zarif)

如果我們想要無回授 FIR 濾波器的方塊圖，y[n] 就會是第一次加總的結果 (圖 4)。

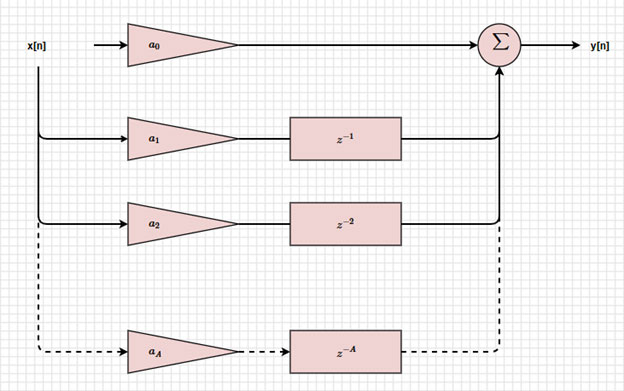圖 4：FIR 濾波器的方塊圖。(圖片來源：Mustahsin Zarif)

現在我們已經瞭解 FIR 和 IIR 濾波器的基礎知識，讓我們用一個範例來說明學到的內容：移動平均濾波器。

移動平均的運作方式是採用當前的輸入加上特定數量的先前輸入後加以平均 (方程式 3)。

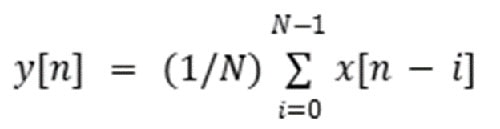方程式 3：移動平均方程式。(圖片來源：Mustahsin Zarif)

其中 N= 影響輸出的樣本視窗大小／數量

我們可以看到這是一個 FIR 濾波器，因為方程式的右側沒有 y 項。

但是，我們可聰明地重新排列方程，以構成 IIR 濾波器。試想以下項目：

讓 N=5，可得到

y[5] = (x[5]+x[4]+x[3]+x[2]+x[1])/5，

以及 y[6] = (x[6]+x[5]+x[4]+x[3]+x[2])/5

y[6]=(x[6]+y[5]-x[1])/5

因此，當前輸出現在就取決於前一個輸出 (y[6] 取決於 y[5])！

更簡單來說，

y[n] = (y[n − 1] + x[n] − x[n − N - 1])/N

其中 N = 視窗大小

這個濾波器在平滑時域訊號方面的效果很好，如圖 5 所示，那時我以視窗大小 N = 11 用 python 進行模擬。

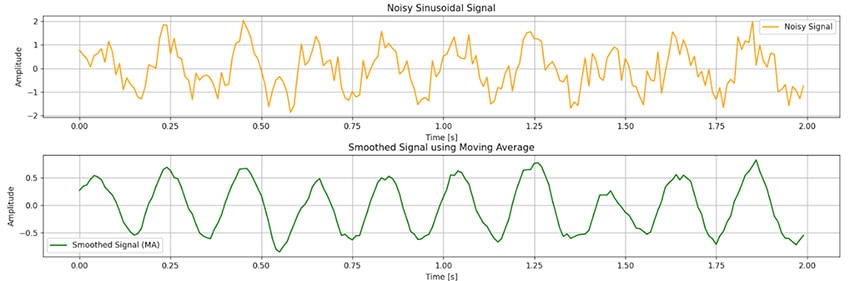圖 5：使用 Python 進行移動濾波器模擬。(圖片來源：Mustahsin Zarif)

移動濾波器模擬的 Python 程式碼：

複製import numpy as np

import matplotlib.pyplot as plt



# Parameters for the sinusoidal wave

frequency = 5  # in Hertz

sampling_rate = 100  # Sampling rate in samples per second

duration = 2  # in seconds



# Generate time axis

t = np.linspace(0, duration, int(sampling_rate * duration), endpoint=False)



# Generate a clean sinusoidal signal

clean_signal = np.sin(2  np.pi  frequency * t)



# Add random, white (Gaussian) noise to the signal

noise_amplitude = 0.5

noisy_signal = clean_signal + noise_amplitude * np.random.normal(size=t.shape)



def moving_average(signal, window_size):

    window = np.ones(window_size) / window_size

    return np.convolve(signal, window, mode='same') 



# Apply moving average to the noisy signal

window_size = 11

smoothed_signal_ma = moving_average(noisy_signal, window_size)



# Plot the noisy and smoothed signals

plt.figure(figsize=(12, 9))



plt.subplot(2, 1, 1)

plt.plot(t, noisy_signal, label='Noisy Signal', color='orange')

plt.title('Noisy Sinusoidal Signal')

plt.xlabel('Time [s]')

plt.ylabel('Amplitude')

plt.grid(True)

plt.legend()



plt.subplot(2, 1, 2)

plt.plot(t, smoothed_signal_ma, label='Smoothed Signal (MA)', color='green')

plt.title('Smoothed Signal using Moving Average')

plt.xlabel('Time [s]')

plt.ylabel('Amplitude')

plt.grid(True)

plt.legend()



plt.tight_layout()

plt.show()

總結

本部落格的開頭說明資料在現實世界中受到雜訊破壞的情況。雖然我們無法得到如同數學方程式般預期的理想回應，但仍可將收集到的數據過濾掉不想要的特徵，以盡可能符合理想回應。有多種方法可達到此目標，且在許多情境下，我們會想要這樣做。本文最後展示了移動平均濾波器的模擬回應，在下一篇文章中，我們將探討指數式移動平均濾波器如何平滑雜訊慣性測量單元 (IMU) 的數據！