Not All Noise is Bad: Why and How to Use Noise for Test and Circuit Applications

Electronics engineers and technicians are accustomed to regarding noise as a negative and so optimize for low noise during component selection, circuit design, and board layout. The fact is that sometimes random or pseudo-random noise can be useful. Let’s look more closely to see why—and how to take advantage of it.

There are two types of random noise that are commonly used in a variety of applications; white noise and pink noise. White noise has a flat frequency spectrum with equal power—measured in decibels (dB)—over its bandwidth. Pink noise has equal power over each frequency octave within its bandwidth (Figure 1).

Figure 1: Comparing the frequency spectra of white and pink noise. The power spectrum of white noise is flat, while the power spectrum of pink noise decreases at 3 dB per octave. (Image source: Art Pini)

Pink noise, because it approximates the response of the human ear, is used for audio testing and sound-system equalization.

Room equalization adjusts the frequency response of a sound system to produce exactly the same signal which is put into it. If you put pink noise into the sound system, the equalizer is adjusted to get pink noise out, as measured on a spectrum analyzer (Figure 2).

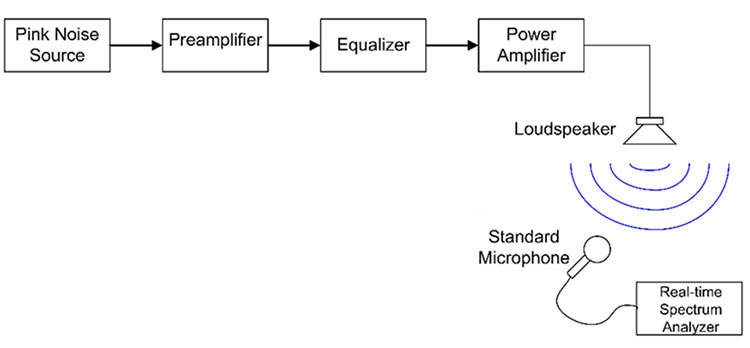Figure 2: The frequency response of the room is adjusted using the equalizer to reproduce the input without loss or distortion. (Image source: Art Pini)

White noise is used for measuring frequency response and as a spreading source for spread-spectrum communications.

Consider the following example, which characterizes the frequency response of a 10.7 megahertz (MHz) intermediate frequency (IF) filter (Figure 3).

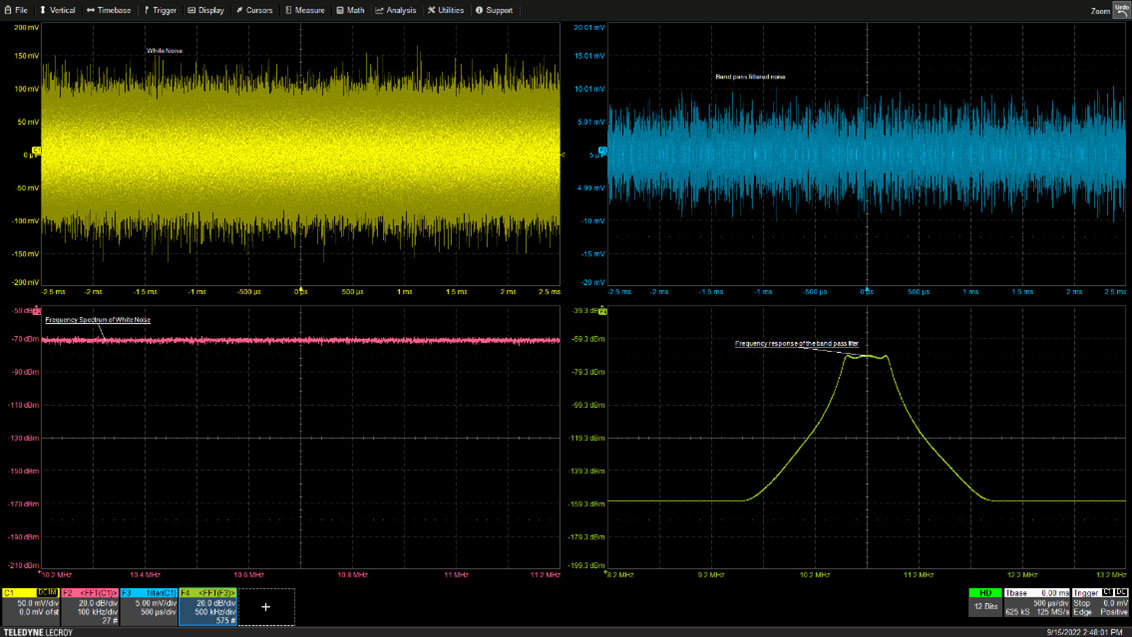Figure 3: Using broadband white noise to measure the frequency response of a 10.7 MHz IF filter. (Image source: Art Pini)

White noise, shown in the upper left grid, is fed into the filter through an appropriate impedance-matching network. The frequency spectrum of the input is shown in the lower left grid, which is flat over the whole range of frequencies of interest. The properly terminated filter output is shown in the upper right grid. It has a lower amplitude than the input because the bandpass filter has attenuated the frequency components outside of the filter’s bandwidth. The frequency spectrum of the filter output, in the lower right grid, shows the filter has a bandwidth of about 400 kilohertz (kHz) at a center frequency of 10.7 MHz. The theoretical frequency response is the complex ratio of the output signal to the input signal. Since the input signal magnitude is uniform, the output spectrum shows the magnitude spectral response of the filter.

Constructing a noise generator

Noise generators can be based on any of three basic technologies. The first is to use the Johnson noise produced in resistors. This electronic noise is generated by the thermal agitation of the electrons inside an electrical conductor, which happens regardless of any applied voltage. The noise produced is essentially white Gaussian noise, which has to be buffered by some very high-gain amplifiers.

The second method is to use a reverse-biased Zener or avalanche breakdown diode. This noise is also white and has a higher level than Johnson noise, but still requires high-gain amplifiers.

The third method is to generate a pseudo-random binary sequence (PRBS) using a shift register, along with a digital-to-analog converter (DAC) and a filter to convert the PRBS into white noise. The PRBS noise stream has a finite length that repeats. The length can be set by the number of shift register stages. The reciprocal of the signal duration is the lowest frequency that can be reproduced by the PRBS generator. The PRBS generator offers the highest output voltage and doesn’t require high-gain amplifiers.

The PRBS generator can be implemented with discrete shift registers as shown in Figure 4, or with a programmable system-on-chip, such as a microcontroller or FPGA.

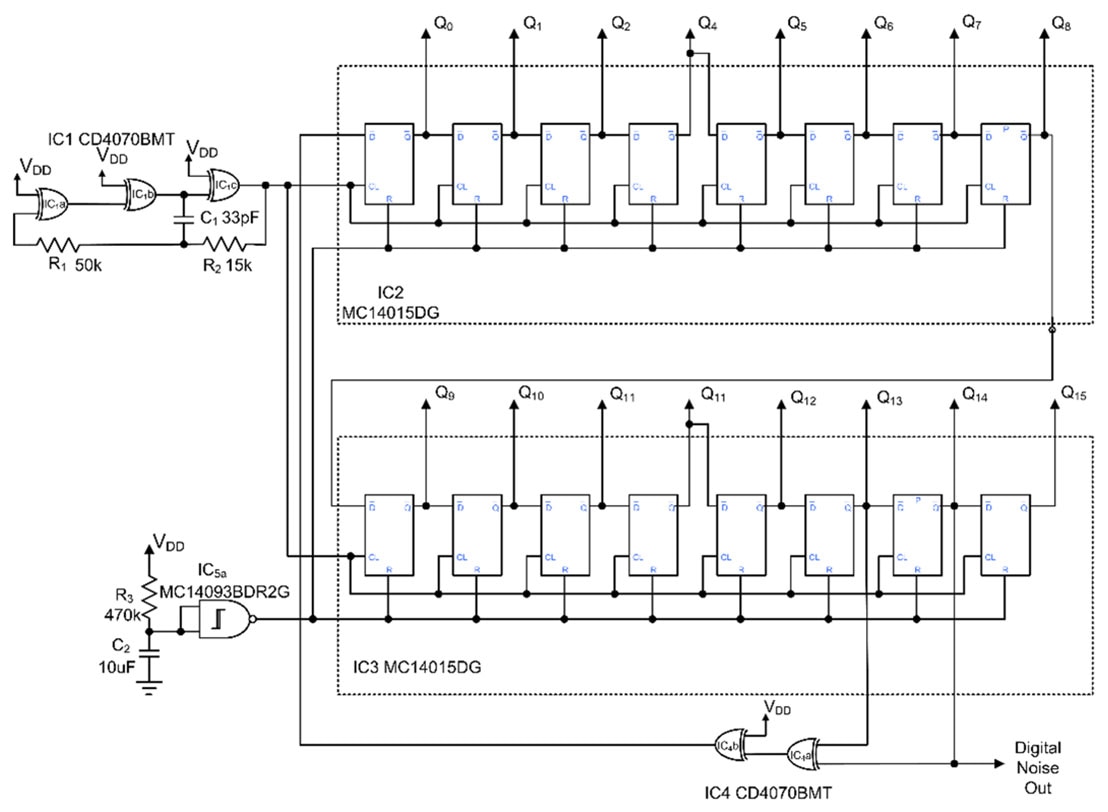Figure 4: The implementation of a 16-bit PRBS noise generator using two discrete octal D-type flip-flop ICs. (Image source: Art Pini)

The low-cost PRBS generator design shown in Figure 4 is based upon a linear feedback shift register implementation that uses onsemi’s MC14015DG dual 4-bit static shift register and Texas Instruments’ CD4070BMT quad XOR gate. Sixteen D-type flip-flops (eight per IC)—with feedback taps at the 14th and 15th—produce a PRBS15 data pattern. The feedback connection is via an XOR gate. This data pattern has a length of 32767 bits, which is a duration of about 65 milliseconds (ms) at a 500 kHz clock rate. Longer patterns can be achieved by using more shift registers, with an appropriate change in the feedback taps.

The generator is initialized to the “all zeros” state at power up using an onsemi MC14093BDR2G Schmitt trigger NAND gate (IC5) and a basic resistor-capacitor (RC) network. The clock is provided by a simple CMOS oscillator running near 500 kHz. The digital output can be taken from any of the shift register Q outputs. In this case, Q14 was used.

While an analog filter could be used, it would be restricted to a specific clock frequency. By using a finite impulse response (FIR) low-pass digital filter, the filter cutoff will track any changes in the clock frequency. Additionally, the FIR filter can provide very low cutoff frequencies that would require very large capacitors in an analog filter. The FIR filter combines the weighted sum of the shift register outputs. The weighting required to produce a rectangular low-pass filter response in the frequency domain is sin(x)/x in the time domain (Figure 5).

Figure 5: The output stage of the generator employs sin(x)/x weighted samples from the shift register outputs to implement an FIR low-pass filter. (Image source: Art Pini)

The weighted shift register outputs are summed in the differential amplifier, which comprises three sections of an LM324KDR quad operational amplifier (op amp). The upper resistor bank represents the negative components of the sin(x)/x weighting. The lower resistor bank represents the positive values. This digital filter band limits the output to about 5% of the 500 kHz clock frequency, or 25 kHz, which is suitable for audio frequency test purposes.

The white noise output of this generator can be converted into pink noise using a simple resistor-capacitor filter (Figure 6).

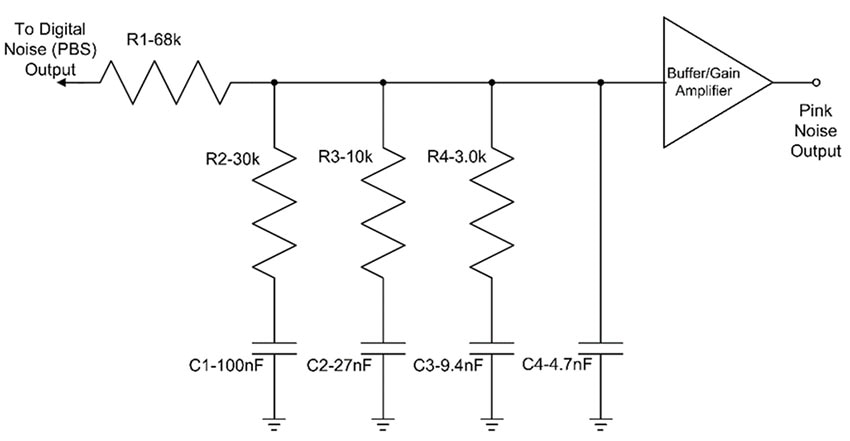Figure 6: This simple RC filter will produce pink noise from the digital noise output of the generator. (Image source: Art Pini)

The amplifier is chosen to match the expected load. This type of noise generator is suitable for audio testing and equalization.

Conclusion

While noise is generally something to be removed or at least mitigated, the right kind of noise can be useful. Due to their known spectral power distribution, white and pink noise are a great resource for frequency-response testing. As shown, using a few off-the-shelf components, an appropriate noise generator can be quickly constructed.