瞭解如何使用切換式電容濾波器來節省空間並提升濾波器效能

來自物聯網 (IoT) 和創客專案的感測器類比訊號，必須先進行某種程度的訊號處理，才能在類比數位轉換器 (ADC) 端進行數位化。然而，這個類比訊號處理階段可能規模很大、昂貴、不準確，而且會隨溫度變化而不穩定。設計人員使用切換式電容濾波器來抗交疊，可大幅減緩這些問題，並簡化設計程序。

感測器訊號在輸入 ADC 之前需要使用抗交疊低通濾波器，確保頻寬已經過正確限制。典型的被動低通濾波器需要龐大的電感和大型電容。對於主動電阻電容 (RC) 濾波器而言，其 RC 時間常數值必須很大。在這兩種情況下，濾波器會變得對 RC 元件容錯和溫度穩定性很敏感。

此外，在積體電路內執行高電阻值時，很難實現合理的準確度。這造成 IC 設計採用外接電阻和電容，也就增加了元件的數量、成本、複雜性和濾波器的體積。

要解決這些問題，設計人員應該考慮採用切換式電容架構，以提高準確度和濾波器的容積效率。這些設計通過提供相同電阻且精準定時的切換元件來控制電容間的電荷轉移。電容及相關的開關很容易採用單晶片的形式。

本文將詳細介紹切換式電容濾波器 (SCF) 的工作原理，說明其如何作為被動和主動濾波器的替代選擇。本文還會介紹範例解決方案，展示如何實作此種濾波器。

什麼是交疊？

ADC 和 DAC 等的取樣資料系統必須符合奈奎斯特標準，該標準聲明元件必須在大於輸入端最高頻率兩倍的頻率下取樣。如果違反奈奎斯特標準，在過低的頻率下取樣，則濾波器的頻率通帶中會出現不理想的雜散訊號 (圖 1)。

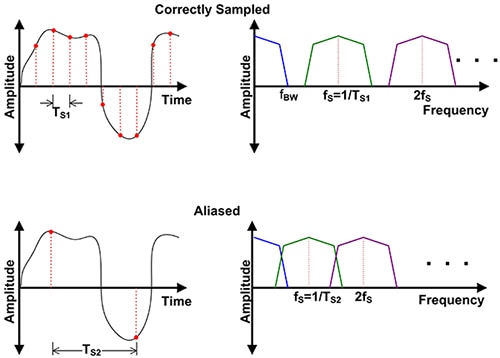
圖 1：當取樣率小於輸入訊號頻寬的兩倍時產生的交疊。與取樣頻率對應的下邊帶影像訊號成分會外差入基頻訊號，導致無法消除的失真問題。(圖片來源：DigiKey)

上圖顯示以大於訊號頻寬兩倍的頻率取樣的時域訊號 (左)。右方的頻域檢視圖則顯示 DC 到 f_BW 的基頻訊號與取樣頻率 f_S 下邊帶影像相互分離。

下圖顯示交疊的情況。時域訊號 (左) 的取樣低於訊號頻寬的兩倍，違反了奈奎斯特標準。在頻率光譜 (右) 中，取樣頻率向左移，反映出較低的取樣率。取樣時脈影像的下邊帶現與基頻訊號重疊，產生的雜散訊號污染了光譜。一旦發生此情況，原始訊號將再也無法復原。

有兩種常用的方法可以防止交疊。一種是使用低通濾波器對 ADC 的輸入進行頻寬限制。這種方法需要用到切換式電容濾波器 (SCF)。另一種方法是將取樣率提高到能確保取樣率大幅超過輸入訊號頻寬。

配置成低通濾波器的 SCF 在預防交疊方面可圈可點，但由於也是取樣資料系統，因此必須符合奈奎斯特標準。但是為避免發生交疊，SCF 要求取樣頻率必須是輸入訊號頻寬的 50 至 100 倍。如此可提供充足的護衛頻寬來防止發生交疊。如果使用較低的取樣頻率，則可在 SCF 之前使用簡易的抗交疊濾波器來防止交疊。在大多數情況下，這些濾波器就和單極 RC 低通濾波器一樣簡單。

切換式電容與連續時間濾波器的比較

使用一個簡單的單極 RC 低通濾波器，即可輕鬆比較 SCF 和連續時間濾波器 (圖 2)。

圖 2：將連續時間 RC 低通濾波器與 SCF 進行比較，顯示了切換式電容充當電阻。(圖片來源：DigiKey)

頂部的線路圖顯示了一個簡單的單極 RC 低通濾波器。-3 dB 頻寬以方程式 1 來表示：

低頻濾波器截止頻率將需要非常大的電阻值。如果將此類電阻整合到單晶片 IC 中，則電阻容差值會大約介於 20% 至 50%。

圖 1 下方線路圖中所示為同一個低通濾波器的切換式電容實作。開關 S₁ 與 S₂ 由非重疊時脈 j₁ 與 j₂ 所驅動，這兩個時脈的頻率為 f_S。S1 先將輸入電容 C₂ 連接到輸入 V_IN。接著 S₁ 會打開，且 S₂ 會關閉，讓 C₂ 得以與 C₁ 共用電荷。從輸入 (V_IN) 傳到輸出 (V_OUT) 的電荷使用方程式 2 計算：

從輸入流到輸出的平均電流為電荷的時間積分，如方程式 3 所示：

這是歐姆定律定義，針對切換式電容電路的電流。 使用此公式，即可用方程式 4 計算出等效電阻：

因此，對於 200 kHz 的時脈頻率和 5 pF 的切換式電容，等效電阻為 1 MΩ。

將此等效電阻代入單極低通濾波器頻寬的方程式中，我們便得到方程式 5 中所示的 SCF 版本：

在切換式電容配置中，頻寬取決於取樣或時脈頻率，以及切換式電容 C₂ 與積分電容 C₁ 的比值。在單晶片 IC 結構中，電阻由小值電容和開關代替。這兩個元件較容易整合到 IC 中，只佔用晶片上的一小塊區域。

濾波器的截止頻率與取樣時脈頻率成比例，因此時脈可用來調諧濾波器，這就彈性而言是個重要的特點。取樣時脈若使用高品質的來源，能確保時脈頻率準確穩定，從而確保濾波器的角頻率同樣準確穩定。

亦請注意，截止頻率與電容值的比率成比例，該電容值在 IC 結構中可保持小於 0.1% 的容差水平。溫度變化會同時影響電容，並且該比率趨於保持恆定。

切換式電容濾波器的建構基礎

配置為積分器的無功元件，是濾波器的建構基礎。一般來說，在濾波器設計中，每一個積分器可獲得一極。切換式電容取代類比積分器設計中的電阻元件 (圖 3)。

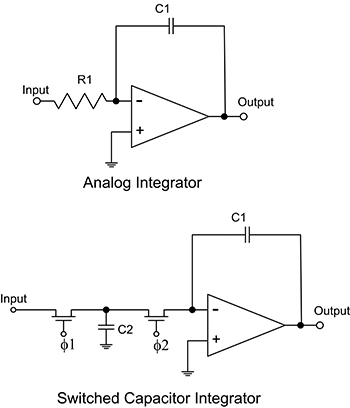
圖 3：切換式電容取代類比積分器中的電阻。開關元件使用雙相時脈驅動的 CMOS FET 來實現。(圖片來源：DigiKey)

切換式電容用於取代類比積分器中的電阻。使用由非重疊 j1 和 j2 時脈驅動的兩個 CMOS FET 完成切換。

實際上，像雙極通用狀態變數設計這樣的類比濾波器可以作為 CMOS 切換式電容濾波器運作 (圖 4)。

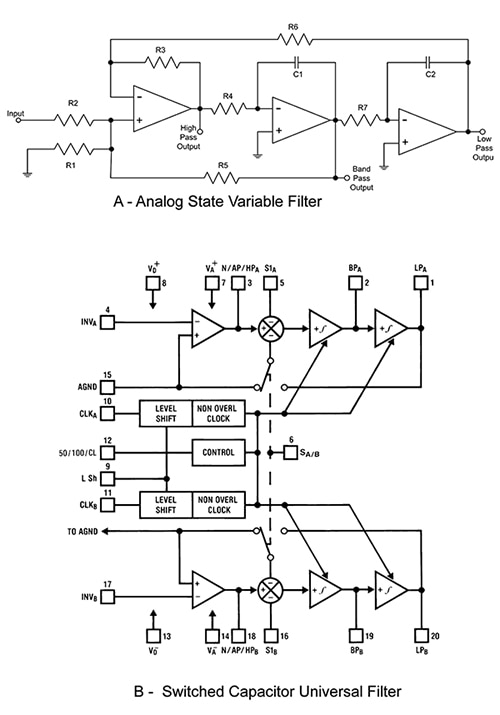
圖 4：雙極狀態變數通用濾波器與 SCF 的比較。 兩者皆為通用濾波器，且都能提供高通、低通和帶通輸出 (圖片來源：DigiKey (A) 和 Texas Instruments (B))

SCF (B) 實際上是 Texas Instruments 的 MF10CCWMX/NOPB 雙通用 SCF 的功能方塊圖。此產品與類比狀態變數濾波器一樣，每個區段都含有兩個積分器級。 此例中為切換式電容積分器。每個區段都能執行最大截止頻率為 30 kHz 的雙極二階濾波器。如果將兩個區段相連接，即可在單一 IC 封裝中產生四階濾波器。該元件不需要任何外接電容，只需要電阻。時脈的頻率必須是目標截止頻率的 50 倍或 100 倍。

SCF 實作的一個示例使用 MF10 的兩個區段建立 1 KHz 低通濾波器 (圖 5)。

圖 5：使用 MF10 SCF IC 實作四階 1 kHz 低通濾波器。(圖片來源：Texas Instruments)

積分與切換式電容都是 20 引腳 IC 的內部元件。電阻是唯一用來設定濾波器屬性的外部元件。此電路設計使用單個 10 V 電源配置 MF10。時脈頻率為 1 kHz 截止頻率的 100 倍。

使用 SCF 進行設計

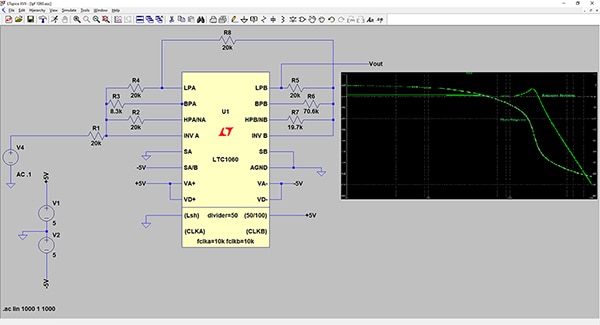
供應商可以提供設計工具來加快設計階段的速度。Analog Devices 的 LTC1060 雙通用濾波器建構模塊 IC 即為一例。該公司的 LTspice XVII 模擬程式支援此 IC (圖 6)。

圖 6：以 Analog Device 的 LTspice XVII 打造的四極低通濾波器設計，顯示了線路圖與頻率／相位響應標繪圖。(圖片來源：DigiKey)

Analog Devices 為 LTC1060 濾波器建構模塊提供了一個 Spice 模型。其為雙通用 SCF IC，工作頻率高達 30 kHz，最大時脈率為 500 kHz。每個濾波段都含有兩個積分器，為每個區段提供雙極。一共有六種操作模式，因此可配置為低通、高通、帶通或帶阻濾波器。設計範例中結合 IC 的兩個區段，建立了一個 4 極 200 Hz 低通濾波器，其時脈頻率為 10 kHz。該設計只用了七個電阻，無任何電容或電感。

除了這些通用濾波器外，一些特定類型的濾波器也會隨附 SCF。各大供應商提供了貝塞爾、巴特沃斯、橢圓及線性相位濾波器配置。

結論

如上所述，SCF 提供精準的頻譜控制，能在積體電路上輕鬆實作。這種濾波器在效能、體積與成本上要比類比 RC 型濾波器為佳，而且主動濾波器不需使用無功元件就具備這些優勢。一大優點是只要改變時脈頻率，就能即時改變濾波器的頻率特性。