How to Apply Ohm’s Law to Series and Parallel Circuits

Let’s start with figuring out what Ohm’s Law even is, and how it applies to what we will go over today. Ohm’s Law was named after Georg Ohm who discovered that current flow through a conductor is directly related to the voltage and resistance. This means that the voltage can be found by multiplying the current and resistance in a circuit or component.

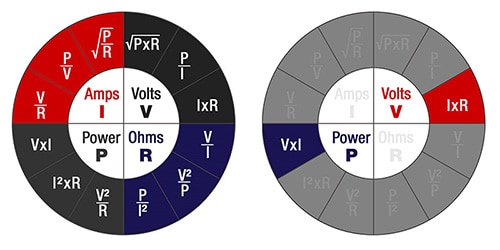
Examples: V=I x R, R=V/I, I=V/R

Where:
V = Voltage
I = Current
R = Resistance

Now, how do we apply this to a circuit? Well, first we must decipher if the circuit is in series or parallel as each has their own rules to come up with a total for each value. The series equations go as such (C below is capacitance):

V_T= V₁+V₂+...

I_T= I₁= I₂= ...

R_T= R₁+R₂+...

1/C_T= 1/C₁+1/C₂+...

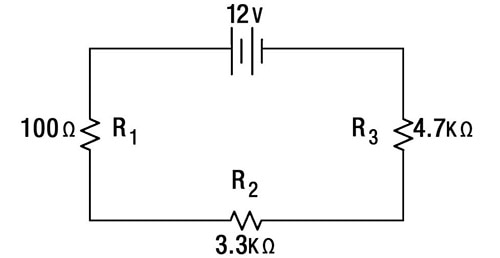
Alright, now the graphic below shows a series circuit with only a couple of values given. Using the series equations above, coupled with Ohm’s law, we can solve for all of the values.

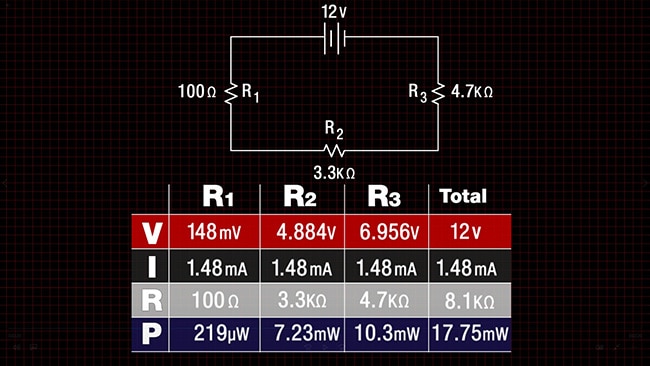
The next graphic shows the table filled in with all of the correct values. Start by adding up the resistance to get the total of 8.1 KΩ. Since we also have the voltage total of 12 V, we can solve for current total as follows: (12 V)/(8100 Ω) = 0.00148 A or 1.48 mA. This current is the same through the entire circuit because everything is in series. Now that we have all of the current values and all of the resistance values, we can solve for all of the voltage totals using V=I x R. To solve for power (P), use P=I x V. Voila, it’s that simple.

Now let’s go over the equations for a parallel circuit:

V_T= V₁=V₂=...

I_T= I₁+I₂+...

1/R_T= 1/R₁+1/R₂+...

C_T= C₁+C₂+...

What has changed? In a parallel circuit the voltage total is equal to the voltage in each line of the parallel circuit. Current is added up to find the total. The equations for resistance and capacitance are switched.

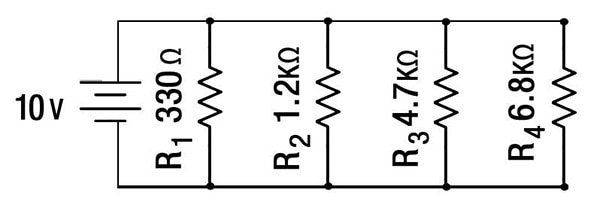
Below is a graphic of a parallel circuit with a few values given. Using the parallel equations above, coupled with Ohm’s law, we can solve for all of the values.

The graphic below is a table with all of the correct values filled in. So far we know the voltage is 10 V, so we have added that across the board. Next we can figure out the resistance total as follows: 1/(330 Ω)+1/(1200 Ω)+1/(4700 Ω)+1/(6800 Ω) = 0.0042234/Ω. Then we take the reciprocal of that total and get 236.96 Ω. To fill in the rest of the board we can use Ohm’s Law. I=V/R will give us each current total. Then use P=I x V again for the power values.

You’ll notice we didn’t use all of the series or parallel equations and instead used Ohm’s Law for some. These can be used in combination to verify that the initial answer is correct. These equations are pertinent when planning any circuit, so it is vitally important to learn if you plan to tinker with electronics. Don’t fret, DigiKey has some online calculators that can help with this. Practice makes perfect. Happy learning!